News

• We actively collaborate with industrial partners for real-world TinyML applications. Feel free to contact Prof. Song Han for more info.
• DGA was accepted by NeurIPS 2021 and the poster session will be at 08:30 to 10:00am PST on Dec 7.

Citation

 @inproceedings{zhu2021dga,
    title     = {Delayed Gradient Averaging: Tolerate the Communication Latency in Federated Learning},
    author    = {Zhu, Ligeng and Lin, Hongzhou and Lu, Yao and Lin, Yujun and and Han, Song},
    booktitle = {Annual Conference on Neural Information Processing Systems (NeurIPS)},
    year      = {2021}
} 

Abstract

Federated Learning is an emerging direction in distributed machine learning that enables jointly training a model without sharing the data. Since the data is distributed across many edge devices through wireless / long-distance connections, federated learning suffers from inevitable high communication latency. However, the latency issues are undermined in the current literature [15] and existing approaches suchas FedAvg [27] become less efficient when the latency increases. To overcome the problem, we propose Delayed Gradient Averaging (DGA), which delays the averaging step to improve efficiency and allows local computation in parallel to communication. We theoretically prove that DGA attains a similar convergence rate as FedAvg, and empirically show that our algorithm can tolerate high network latency without compromising accuracy. Specifically, we benchmark the training speed on various vision (CIFAR, ImageNet) and language tasks (Shakespeare),with both IID and non-IID partitions, and show DGA can bring 2.55$\times$to 4.07$\times$speedup. Moreover, we built a 16-node Raspberry Pi cluster and show that DGA can consistently speed up real-world federated learning applications

Problem: Federated Learning Suffer from High Latency Communication

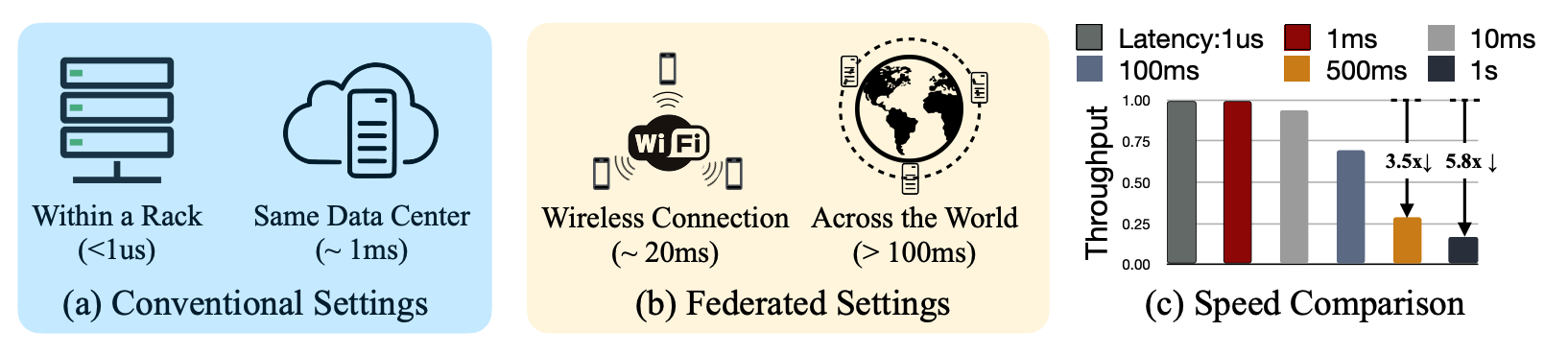
The training settings of conventional distributed training v.s. federated learning are very different. High latency cost greatly degrades the FedAvg’s performance, proposing a severe challenge to scale up the training system. We need to design algorithms to deal with the latency issue.

Algorithm: Delay the Averaging to a Later Iteration

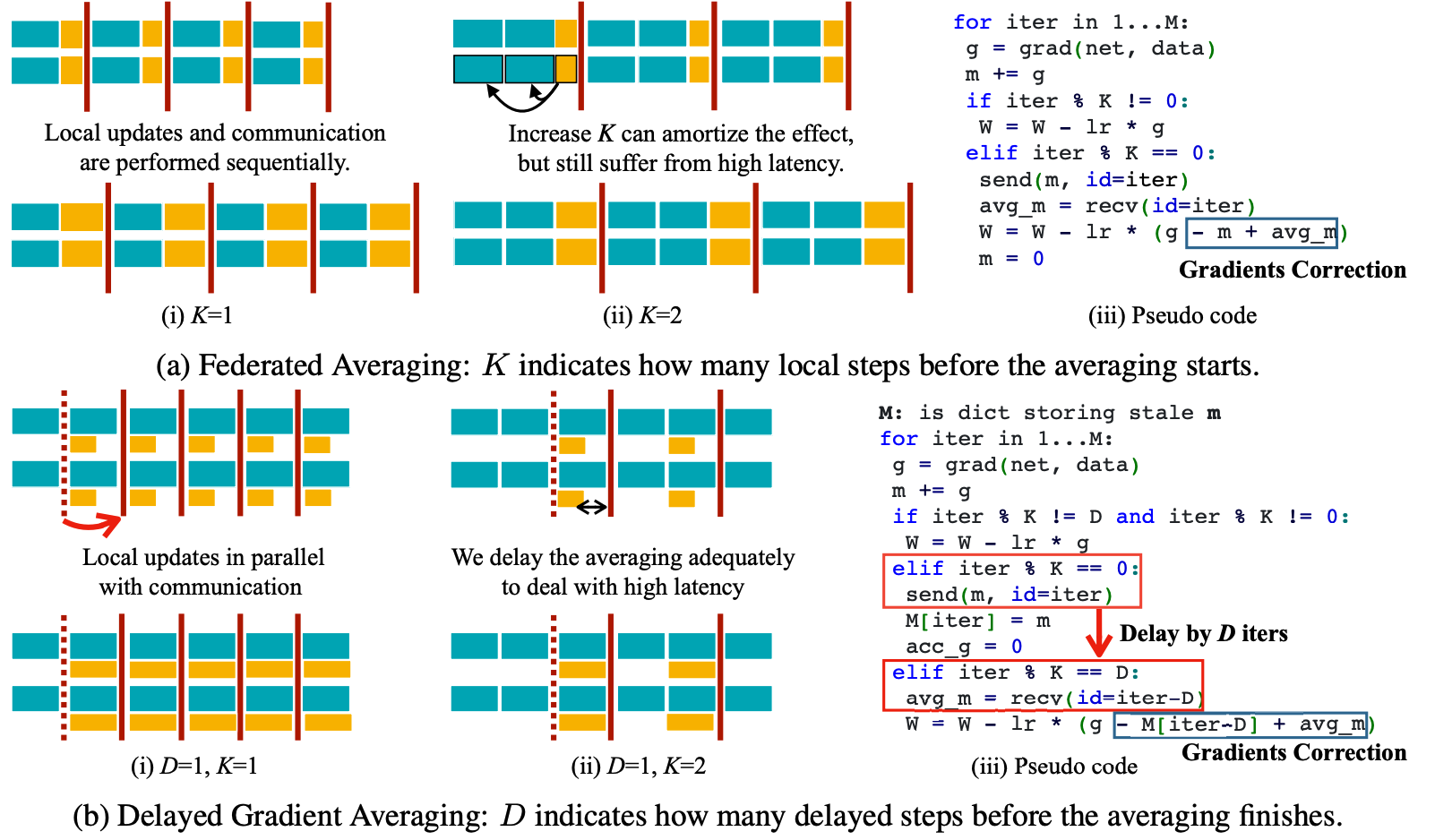
The flatten view of our algorithm. The averaging occurs periodically with period K and the delay parameter D naturally shows up indicating the number of gradients between the sending and reception. The cyan cube in the visualization (a,b) indicates local computation and the yellow cube represents the transmission of the averages. The red bar indicates when the averaging is actually performed. In DGA, the transmission is in parallel to the computation, which is the main reason why DGA can tolerate high latency.

Convergence Analysis

• Assumption 1: The loss function $F(w; x,y )$is Lipchitz smooth $$ \nabla f_{j} (x) - \nabla f_{j} (y) || \le L ||x - y||. \quad \forall x,y \in \mathbb{R}^d $$
• Assumption 2: Bounded gradients and variances $$ E_{\zeta_{j}} || \nabla F_{j} (w; \zeta_{i}) || ^ 2 \le G^2, \forall w, \forall j, $$ $$ E_{\zeta_{j}} || \nabla F_{j} (w; \zeta_{j}) - \nabla f_{j} (w) || ^ 2 \le \sigma^2, \forall w, \forall j. $$

The convergence rate of DGA is $ O (\frac{\Delta+\sigma^2}{\sqrt{JN}}+ \frac{Jd^2}{N}) $ (details in paper).

When $ D < O(N^{\frac{1}{4}} J^{-\frac{3}{4}}) $, DGA converges as fast as original SGD which is $ O (\frac{\Delta+\sigma^2}{\sqrt{JN}}) $.

Note: $ D $ is the number of iterations and $ J $ is the number clients / workers.

Accuracy Analysis

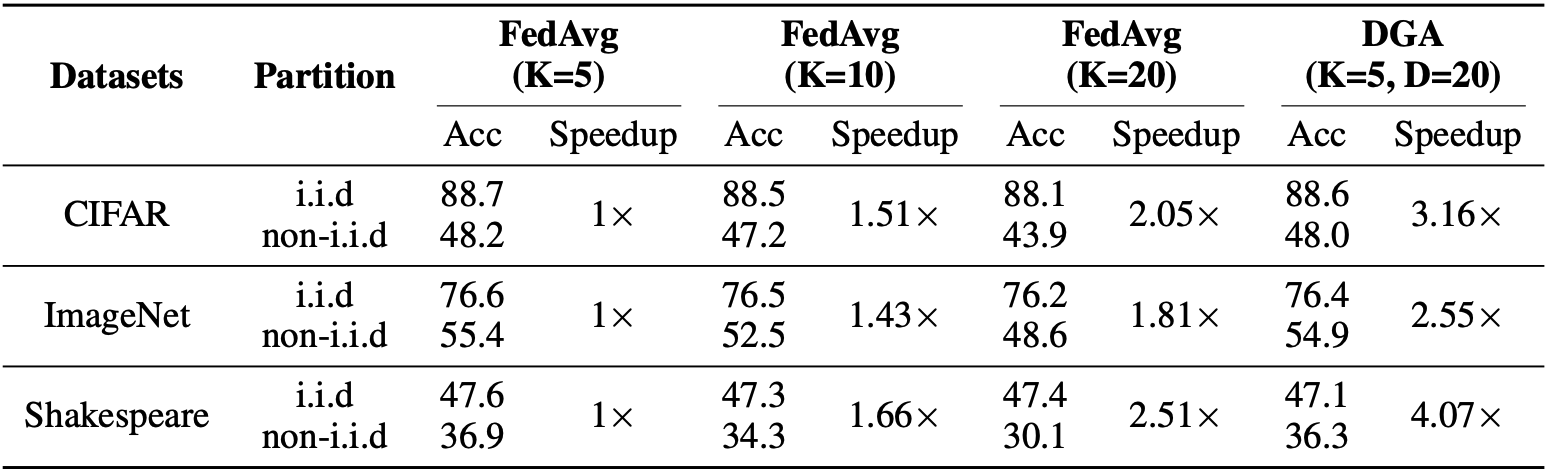
Comparison of FedAvg and our DGA’s accuracy on 3 datasets with both i.i.d and noni.i.d partitions. The speedup is measured on latency with 1s latency. Not only DGA demonstrates consistent training speedup, but also DGA maintains the accuracy, on both i.i.d and non-i.i.d partition.

Speedup Analysis

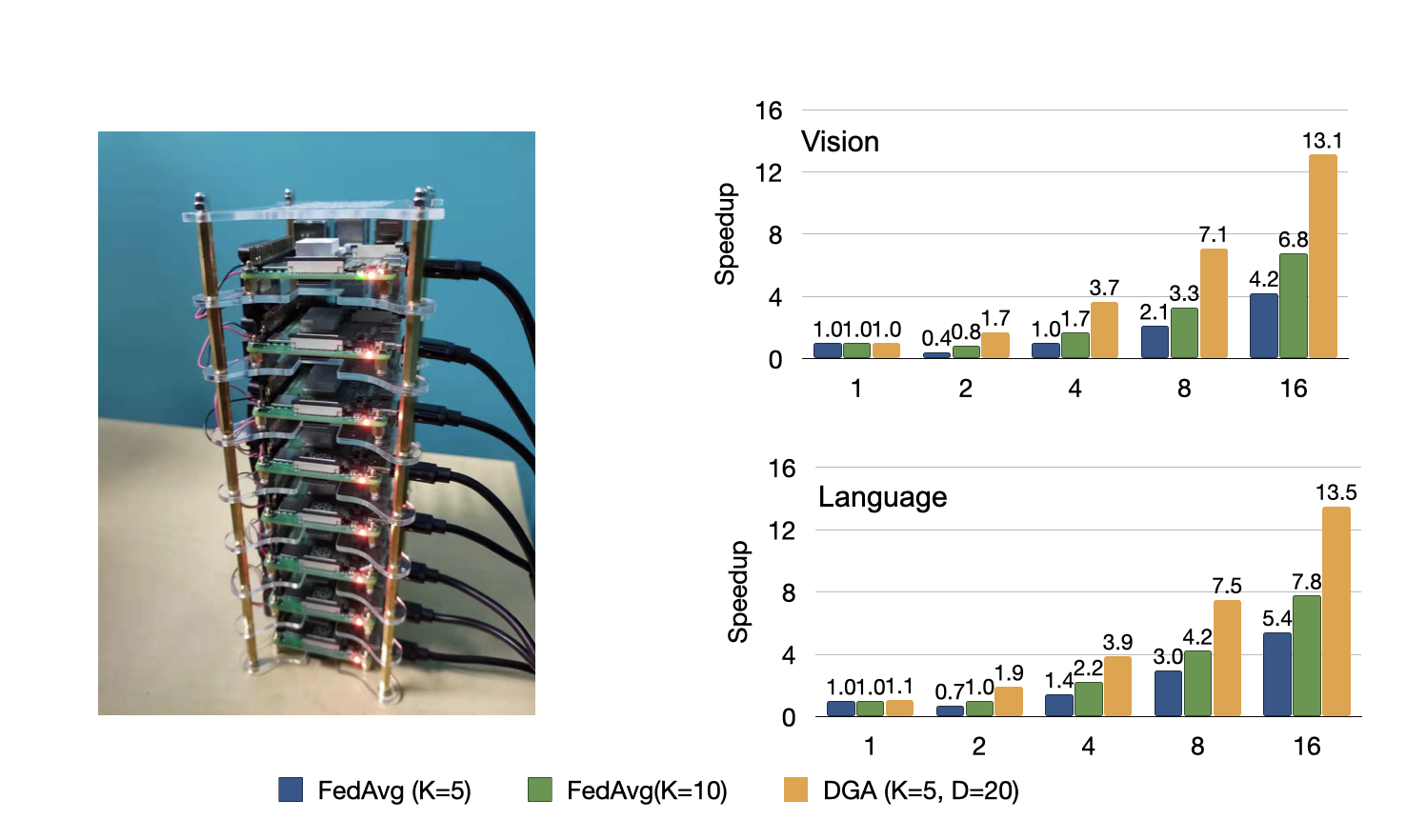
Left: Our Raspberry Pi farm. Experiments are conducted on two racks. Right: The speedup comparison between FedAvg and DGA~on Raspberry Pi cluster. On both vision and language tasks, DGA demonstrate consistent improvement over FedAvg.

Acknowledgments: We thank MIT-IBM Watson AI Lab, Samsung, Woodside Energy, and NSF CAREER Award #1943349 for supporting this research. Hongzhou Lin acknowledges that the work is done prior to joining Amazon. Yao Lu acknowledges that the work is done prior to joining Google.